maldcope

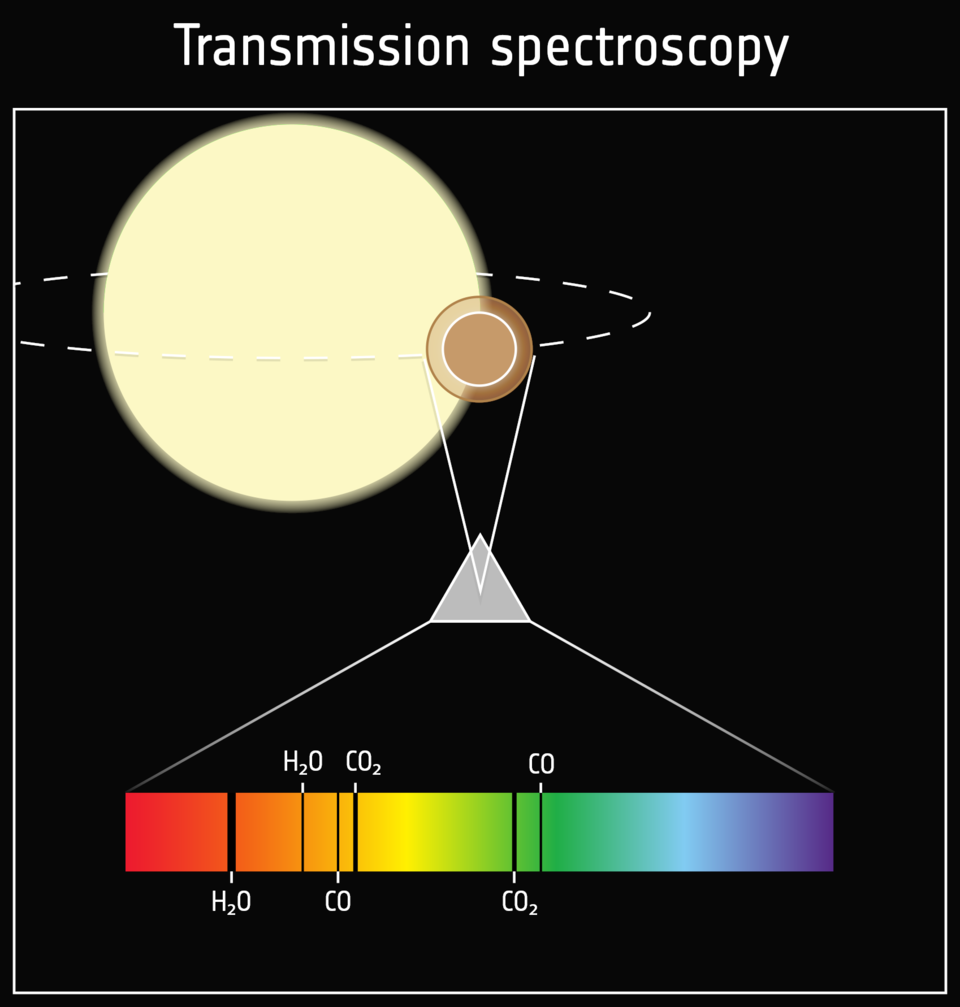
Ariel will take transmission spectra of thousands of exoplanets. Atmospheric retrieval algorithms will not be able to characterize them all, or even a small fraction of them due to the computational resources required to perform a single retrieval. Instead, we need methods that make use of our total knowledge of the exoplanet atmospheres and transmission spectroscopy and can be used for fast and reliable inference.

To this end I implement several SOTA simulation-based inference (SBI) methods, all based Neural Posterior Estimation (NPE) Normalizing Flows (NF). A large part of the challenge is the misspecified model and out-of-distribution (OOD) test data. In addition to this the “ground-truth” traces were obtained by MultiNest in combination with Taurex, which is suspected to be overconfident (under-dispersed). Lastly, the ground-truth traces and the forward model (FM) parameters show significant divergence so that the data, parameterized by the forward model, is misspecified twice, once by the limitations of Taurex and once by the limitations fo the MultiNest retrieval. To address the OOD and missspecification problem the methods need to be robust and amortized, deal well with conflicting distributions of training data, and learn informative features from few (or one) samples.

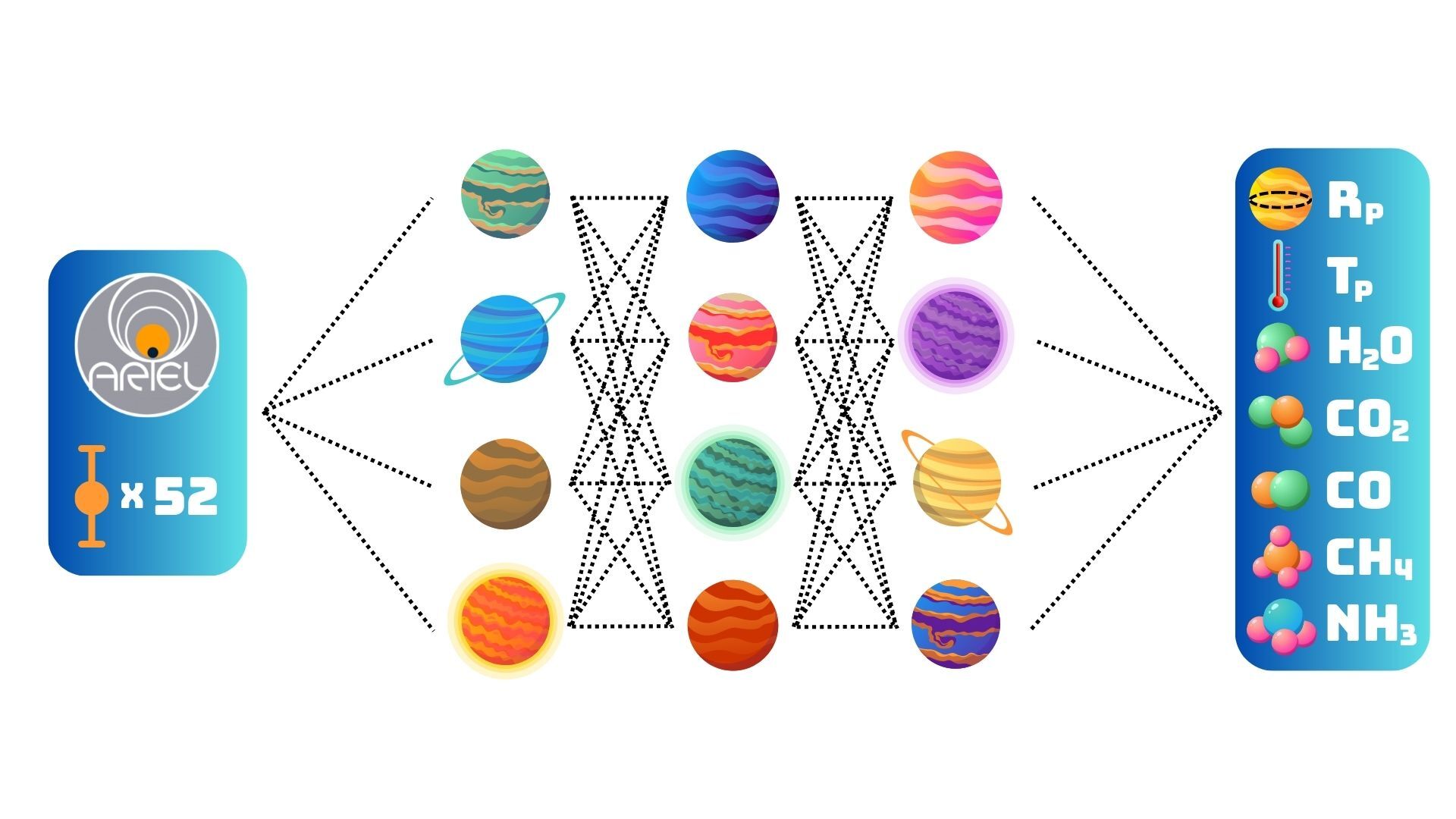
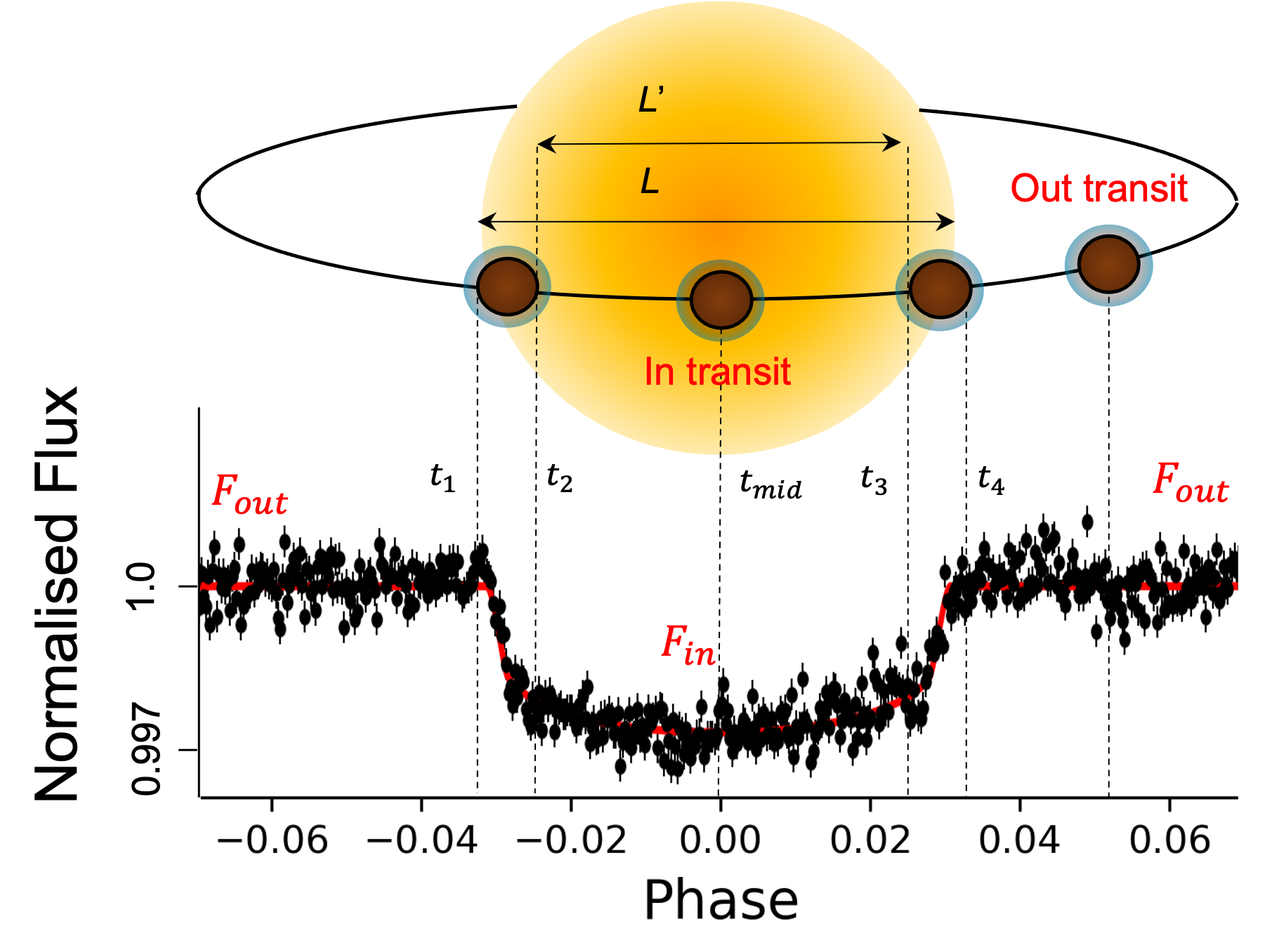
I transform the spectral and truth data to be better suited to the ML domain, i.e. lie between -1 and 1, STD rescaling etc. For the spectral data this is accomplished using a Yeo-Johnson power transform. All input spectral data is augmented with the jointly transformed uncertainties, which increases sample diversity and accurately reflects the uncertainties in the observations. I developed this transform specifically for DL with spectral data, which was previously an unsolved problem in exoplanet science. You can find the uncertainty transformer separately to maldcope on my GitHub.

NPE with KL divergence: This is my baseline solution which is trained on both the trace and FM theta (truth) and uses the KL divergence as its loss. The model was initially based on the work of Vasist et al. 2023, but uses a multimodal embedding to break some degeneracies by using auxiliary data. Extending this idea to using Hierarchical NPE (Rodrigues et al. 2021) would be the logical next step for increasing the effectiveness of the auxiliary data to break degeneracies. The inputs (spectrum, auxiliary) are embedded first separately via a ResCNN and a ResNet before being jointly embedded with a ResNet. The embedding is fed to an NPE using Unconstrained Neural Autoregressive Flows (UNAF) to exploit their ability to generalize well when over-parameterized in its hidden layers.

Robust-NPE with Maximum Mean Discrepancy (MMD): As pointed out previously the KL divergence is a relatively poor estimator for SBI, and it is arguably incompatible with drawing from and inferring complex, multimodal distributions due to the mode collapse problem which makes its use suspect in retrievals. Several solutions such as using Importance Sampling with alpha-Renyi divergence have been proposed (alpha-DPI: Sun et al. 2022). Instead, this model uses the MMD via reparameterized NPE samples and the kernel trick to robustly estimate the difference in moments of the reparameterized distributions. I implement both Radial Basis Function (RBF) and Polynomial Kernel for the reparameterization. I observe that im practice the Polynomial Kernel is more robust, however this might be due to my hyperparameter choices. Since evaluating the MMD in high dimensions with large sample sizes is costly, I anneal a balanced KLD and MMD loss during training. This stabilizes initial training due to the limited sample size and focuses the later training stages more on fitting the higher moments of the distributions compared to their mean.

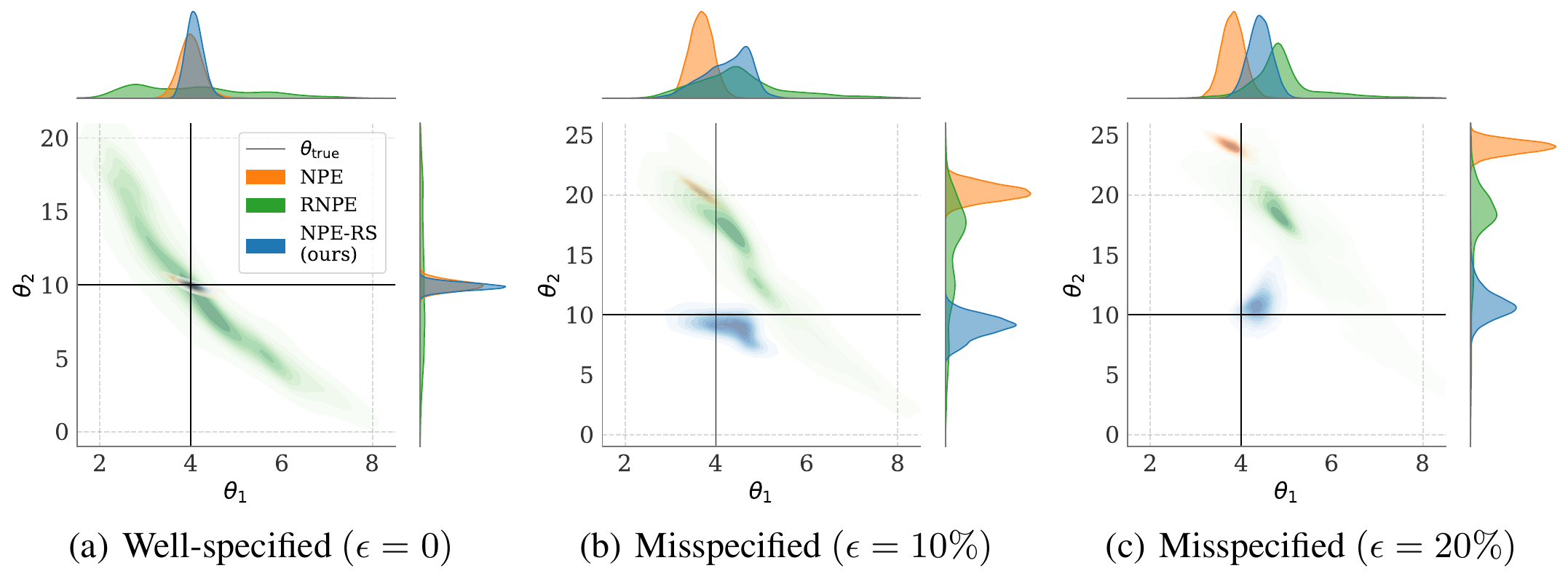
Robust-NPE with d-dimensional Kolmogorov-Smirnov Test (ddKS) The score function for the data challenge relies on the KS test. I believe this to be a contentious choice as the traces of MultiNest should be seen as suspect for retrievals. This is highlighted by the difference between forward model parameters and traces which can be several order of magnitude in the abundances. Still, I expect a two sample test be a powerful tool to archive a high score. To this end I used the d-dimensional Kolmogorov-Smirnov Test (ddKS) to test the R-NPE reparameterized samples against the traces.

Note on the last algorithm; I think this would actually allow us to quantify the underdispersion of e.g. MultiNest with our retrieval algorithms. I would like to have a look into that when I find the time.